前回はデータの共分散行列の表しかたについてまとめました。共分散行列は、要素ごとの分散と、要素間の相関関係を表す行列です。
では、白色化の目的である【要素間の相関をなくす】とはどういうことでしょうか。 下は\(n \times n\)の共分散行列です。
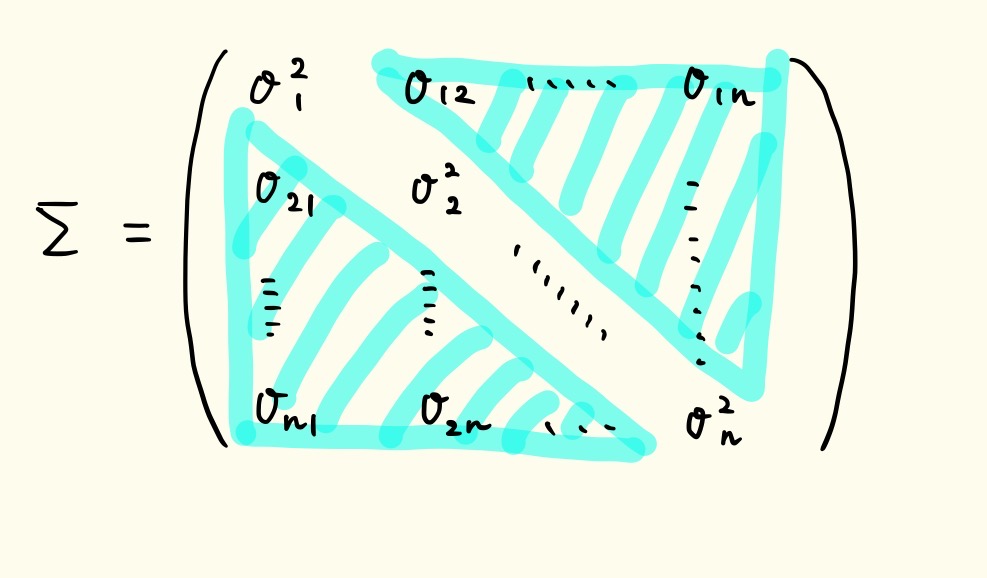
行列内の非対角成分(水色部分)は要素間の相関関係を表し、ここがゼロでない=各成分間で相関があるということです。したがって、この共分散行列を対角成分以外がゼロ、つまり共分散成分がゼロになる対角行列にしてしまえば、各成分が独立となります。
そのために、共分散行列が対称行列になるように元となる特徴空間\( {\it{X}}=(x_1, …, x_n)\)を変形させなければなりません。
言い換えると、特徴空間\(x_n\)に対して、\(D\times D\)行列\( \it {P}\)による線形変換を行い、\( {\it{u}_n}= {\it{Px_n}}\)を作ります。このとき、\({u_n}\)の共分散行列、
$$\Phi_u \equiv \frac{1}{N}\sum^N_{n=1}u_n u_n^T=\frac{1}{N} {\it{UU}^T}$$
が対角行列になるような\(\it{P}\)を定めるということです。
目標とする対角行列を単位行列\(\it{I}\)( \(\Phi_u= \it{I}\) )として、\(\it {P}\)の満たす式べきを求めます。この式は、 \( \it{U}= \it{PX}\)を代入することで、\(\it{P^T P}=\Phi^{-1}_x\)となります。
(多分)導出
この式の過程がよくわからなかったので、自分なりに道筋を考えてみました。
まず、\((\Phi_x=)\frac{1}{N} \it{U U^T}= \it{I}\)に\(\it{U}= \it{PX}\)を代入します。
$$\frac{1}{N} \it{U U^T}= \it{I}\\
\frac{1}{N} \it{PX}( \it{(PX)^T}= \it{I}\\
\frac{1}{N} \it{PX X^T} \it{P^T}= \it{I}$$
右から\( \it{P^{-1}}\)、左から\(\it{({P^T})^{-1}}\)を掛けます。
$$\frac{1}{N} \it{X} \it{X^T} = \it{P^{-1}(P^T)^{-1}}\\
\frac{1}{N} \it{X} \it {X^T}=(\it{P^T} \it{P})^{-1}\\
\frac{1}{N}( \it {XX^T})^{-1}= \it {P^T P}\\
\Phi_x^{-1}= \it {P^T P}$$
導出できました。
途中の式変形に、\(\it{(AB)^T}= \it{B^T A^T}\)と\(\it {(AB)^{-1}}= \it{B^{-1}} \it {A^{-1}}\)を使用。
これで\(x\)の共分散行列から\( \it {P}\)が求められることがわかりました。
固有値問題への落とし込み
白色化は主成分分析と似た考え方からできています。
主成分分析は、情報を圧縮するために分散が最大となる(つまりデータ間で差がでやすい)軸を調べます。
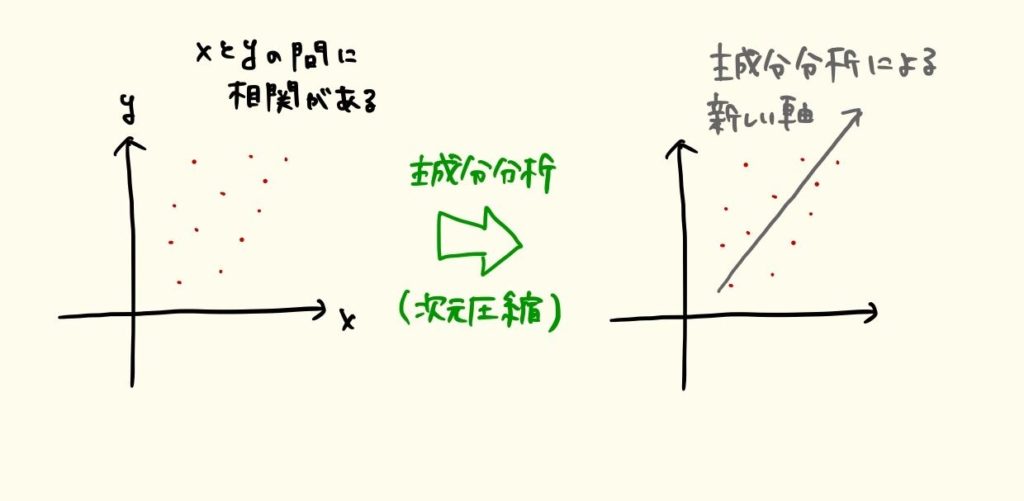
白色化も求めるところは、分散がばらけるようにベクトルを投影しなおすということで共通しています。
主成分分析の軸を求めるのには、固有値問題を解く必要があり、 白色化も同様に、固有値の問題に落とし込むことができるそうです。(主成分分析については、いずれ調べてまとめます)
\(\Phi_x\)を固有値\(D\)と固有ベクトル\(E\)に分解します。
$$\Phi_x= \it{EDE^T}$$
また、\(\it{P^T P}=\Phi_x^{-1}\)より、\( \it{P}= \it{QD^{-\frac{1}{2}}E}\)に変形することができます。なお、\( \it{QQ^T}= \it{I}\)です。
この変形もよくわからなかったので、細かく見ていきます。
まず、\( \it{P^T P}= \it{E} \it{D E^T}\)を以下のように分解します。
$$ \it {P^T P}= \it{ED^{-\frac{1}{2}}} \it{Q^T Q} \it {D^{-\frac{1}{2}}} \it{E^T}$$
\( \it{QQ^T}= \it{Q^T Q} = \it{I}\)なので、このように分解できます。
$$ \it{P^T P}=(\it{Q} \it{D^{-\frac{1}{2}}} \it{E})^T \it{Q} \it{D^{-\frac{1}{2}}} \it{E^T}\\
\it{P}= \it{Q} \it{D^{-\frac{1}{2}}} \it{E^T}$$
ということだと思います。
ただし、ここでは\(\it{QQ^T}= \it{Q^TQ} = \it{I}\)以外に\( \it{Q}\)に対する制約はなく、\( \it{P}\)は\( \it{Q}\)のとりうる値の範囲で複数存在することになります。
PCA白色化
このように、分散が最大になるように各ベクトルを定める(変形する)方法は、前述のように主成分分析(principal component analysis, PCA)に似た考えです。そのため、これをPCA白色化※と呼ぶそうです。
※もしかしたら、本書だけの呼称かもしれません。
ゼロ位相白色化
PCA白色化では自由度を持っていた\(\it{Q}\)に対し、\( \it{P}\)を対称行列(\( \it{P}= \it{P^T}\))に制限することで、一意に定める考えがあります。
式は以下のように、固有値と固有ベクトルだけで表されます。
$$ \it{P_{ZCA}}= \it{ED^{-\frac{1}{2}} E^T}$$
この式変形の過程は、以下のようになります。
$$ \it{PP^T}= \it{ED^{-1} E^T}\\
\it{P^2}= \it{ED^{-\frac{1}{2}} E^T ED^{-\frac{1}{2}} E^T} = ( \it{ED^{-\frac{1}{2}}E^T)^2}$$
ここで、\( \it{EE^T}= \it{E^T E}= \it{I}\)を使っています。
このような白色化は、ゼロ位相白色化(zero-phase whitening)もしくは、ゼロ位相成分分析(zero-phase component analysis, ZCA)などと呼びます。
名前の由来は、\(\it {P}\)の各行ベクトルを\(x\)に適用するフィルタと見たとき、それが対称であること(ゼロ位相であること)に由来するそうですが、よく理解できませんでした。
前処理に関してはかなり面倒そうですが、関数で提供されていたりするのでしょうか?
